图论

图的存储结构

• 邻阶矩阵：利于表示边的权值，O(1)判断两边是否相连，O(N)判断与顶点相连的所有边
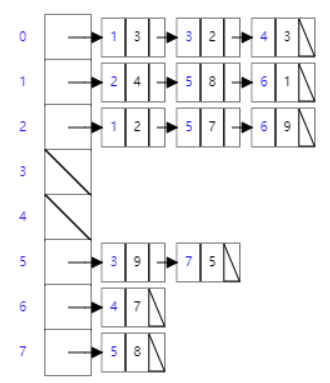
• 邻阶表：vector保存顶点，并将相邻的点用链表串联。利于查找一个顶点的所有边，但不利于确定顶点是否相连以及边的权值

最小生成树

无向图中，任意一对顶点都是连通的，则称为连通图。

n个顶点的连通图的生成树有n-1条边（最小连通子图即为生成树）

构成生成树的所有边权值和最小——最小生成树

Kruskal算法

• 恰好选用n-1条边，权值最小且不能构成回路
• 最小生成树不一定唯一

思路：从边的权值最小处开始选择，并将相连的两个顶点加入并查集。使用并查集判断是否有环，在同一个集合的边不能选择。

::: 示例代码

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <functional>
using namespace std;

struct Edge {
    size_t srcpoint;
    size_t despoint;
    int weight;

    Edge(size_t srcp, size_t desp, int w) : srcpoint(srcp), despoint(desp), weight(w)
    {}

    bool operator> (const Edge& eg) const {
        return weight > eg.weight;
    }
};

int Kruskal(const vector<vector<int>>& matrix, vector<vector<int>>& minTree) {
    priority_queue<Edge, vector<Edge>, greater<Edge>> minHeap;
    int n = matrix.size();

    for(size_t i = 0; i < n; i++) {
        for(size_t j = 0; j < n; j++) {
            if(i < j && matrix[i][j] != INT_MAX) { // 无向图遍历一半就可以了——对称的；i==j无效
                minHeap.push({i, j, matrix[i][j]}); //入队列进行排序
            }
        }
    }

    vector<int> unionfindSet(n, - 1); //并查集
    function<int(int)> findroot = [&unionfindSet](int a)->int{
        while(unionfindSet[a] >= 0) {
            a = unionfindSet[a];
        }
        return a;
    };

    function<void(Edge)> addTree = [&minTree](const Edge & eg) { //添加点到最小生成树
        minTree[eg.srcpoint][eg.despoint] = eg.weight;
    };


    int Nedge = 0;
    int SumWeight = 0;
    while(!minHeap.empty()) {
        Edge Min = minHeap.top();
        minHeap.pop();
        
        int root1 = findroot(Min.srcpoint);
        int root2 = findroot(Min.despoint);
        if(root1 != root2) {
            unionfindSet[root1] += unionfindSet[root2];
            unionfindSet[root2] = root1;  //添加到并查集

            addTree(Min);
            Nedge++;
            SumWeight += Min.weight;
        }
    }

    if(Nedge == n-1) {
        return SumWeight;
    }
    return 0;

}


int main()
{
    vector<vector<int>> matrix {{1, 1, 2}, {1, 0,3}, {2, 3, 0}};
    int n = matrix.size();
    vector<vector<int>> minTree(n, vector<int>(n, 0)); //记录最小生成树

    cout << Kruskal(matrix, minTree) << endl;
    for(auto x : minTree) {
        for(auto y : x) {
            cout << y << " ";
        }
        cout << endl;
    }

    return 0;
}

:::

Prim算法

• 算法思路：开始选择一个顶点，选择与这个顶点相连的最小边，将顶点通过这个最小边相连的对应点添加入集合。
• 使用优先级队列获得权值最小的边，将此边对应的顶点插入set（插入的顶点不能是set中曾经出现过的，否则会成环）

::: 示例代码

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <functional>
#include <unordered_set>
using namespace std;

struct Edge {
    size_t srcpoint;
    size_t despoint;
    int weight;

    Edge(size_t srcp, size_t desp, int w) : srcpoint(srcp), despoint(desp), weight(w)
    {}

    bool operator> (const Edge& eg) const {
        return weight > eg.weight;
    }
};

int Prim(const vector<vector<int>>& matrix, vector<vector<int>>& minTree, size_t startPoint) {
    int n = matrix.size();
    unordered_set<size_t> inX;
    unordered_set<size_t> outY;

    function<void(Edge)> addTree = [&minTree](const Edge & eg) { //添加点到最小生成树
        minTree[eg.srcpoint][eg.despoint] = eg.weight;
    };

    inX.insert(startPoint);
    for(size_t i = 0; i < n; i++) {
        if(startPoint != i) {
            outY.insert(i);  //插入不是开始点的所有点
        }
    }

    //选出startPointchu出发的权值最小边
    priority_queue<Edge, vector<Edge>, greater<Edge>> minHeap;
    // 插入队列时先判断这个边的两个顶点是否同时出现在一个队列中（inX或outY）
    // 不在则插入，在则舍弃
    for(size_t i = 0; i < n; i++) { // i == startpoint ?
        if(matrix[startPoint][i] != INT_MAX) {
            minHeap.push({startPoint, i, matrix[startPoint][i]});  //将不是本体外的所有结点入队列
        }
    }

    int Nedge = 0;
    int SumWeight = 0;
    while(!minHeap.empty()) {
        Edge Min  = minHeap.top();
        minHeap.pop();

        if(inX.count(Min.despoint) == 0) // 插入的点若不在集合中，才可插入，不构成环
        {
            addTree(Min);
            inX.insert(Min.despoint);
            outY.erase(Min.despoint);

            for(size_t i = 0; i < n; i++) {
                if(matrix[Min.despoint][i] != INT_MAX && inX.count(i) == 0) {
                    minHeap.push({Min.despoint, i, matrix[Min.despoint][i]});
                }
            }
            ++Nedge;
            SumWeight+=Min.weight;
        }
    }
    if(Nedge == n-1) {
        return SumWeight;
    }
    return 0;
}


int main()
{
    vector<vector<int>> matrix {{INT_MAX, 1, 2}, {1, INT_MAX,3}, {2, 3, INT_MAX}};
    int n = matrix.size();
    vector<vector<int>> minTree(n, vector<int>(n, 0)); //记录最小生成树

    cout << Prim(matrix, minTree, 2) << endl;
    for(auto x : minTree) {
        for(auto y : x) {
            cout << y << " ";
        }
        cout << endl;
    }

    return 0;
}

:::

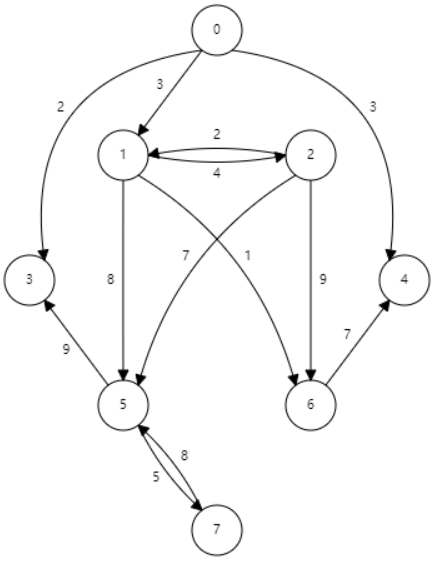
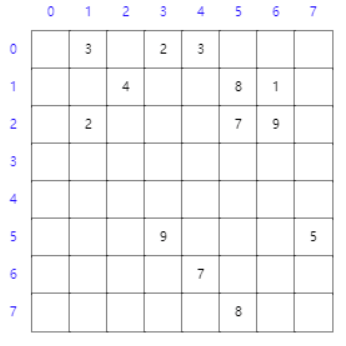
最短路径

带权值的有向图，找到权值和最小的路径

• Dijkstra：针对单源路径，且权值不能为负数

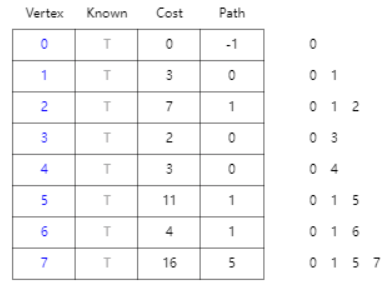
算法思路：选择一个顶点，将顶点连出的所有边对应的节点进行更新，取每次路径权值的和最小值，将权值和最小的点作为下一次更新的起点。

::: 示例代码

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <functional>
#include <unordered_set>
#include <algorithm>

using namespace std;

struct Edge {
    size_t srcpoint;
    size_t despoint;
    int weight;

    Edge(size_t srcp, size_t desp, int w) : srcpoint(srcp), despoint(desp), weight(w)
    {}

    bool operator> (const Edge& eg) const {
        return weight > eg.weight;
    }
};

void PrintShortPath(const size_t& src, const vector<int>& dist, const vector<int>& pPath, int n)
		{
			size_t srci = src;
            vector<char> vertexs {'0','1','2','3','4','5','6','7'};
			for (size_t i = 0; i < n; ++i)
			{
				if (i != srci)
				{
					// 找出i顶点的路径
					vector<int> path;
					size_t parenti = i;
					while (parenti != srci)
					{
						path.push_back(parenti);
						parenti = pPath[parenti];
					}
					path.push_back(srci);
					reverse(path.begin(), path.end());

                    cout <<  vertexs[path[0]] << "到" << vertexs[path[path.size() - 1]]  << "的最短路径为：";
					for (auto index : path)
					{
						cout << vertexs[index] << "->";
					}
					cout <<"权值和为：" << dist[i] << endl;
				}
			}
		}

void Dijkstra(const vector<vector<int>>& matrix, size_t startPoint) {
    int n = matrix.size();
    vector<int> dict(n, INT_MAX); // 记录每个顶点权值和的当前最小值
    vector<int> father(n, -1); //记录当前顶点权值对应的父节点
    vector<bool> Set(n, false); //记录已经遍历过的节点
    dict[0] = 0;
    father[0] = startPoint;

    for(size_t i = 0; i < n; i++) {
        size_t Min = LLONG_MAX;
        size_t Point = 0;
        for(size_t j = 0; j < n; ++j) {
            if(Set[j] == false && dict[j] < Min) { //遍历所有节点，找到节点值比Min小的，作为下次更新的起点
                Point = j;
                Min = dict[j];
            }
        }
        Set[Point] = true; //记录遍历的节点

        for(size_t k = 0; k < n; ++k) {
            //若最小值的点发散出的边，与各个边权值的和小于对应点（K）的值，更新K
            if(Set[k] == false && 
                    matrix[Point][k] != INT_MAX && dict[Point] + matrix[Point][k] < dict[k]) {
                dict[k] = dict[Point] + matrix[Point][k];
                father[k] = Point;
            }
        }
    }

    PrintShortPath(startPoint, dict, father, n);
}


int main()
{
    vector<vector<int>> matrix {{INT_MAX, 3,INT_MAX,2,3, INT_MAX, INT_MAX,INT_MAX}, 
                                {INT_MAX, INT_MAX, 4, INT_MAX, INT_MAX, 8, 1, INT_MAX}, 
                                {INT_MAX, 2, INT_MAX, INT_MAX, INT_MAX, 7, 9, INT_MAX},
                                {INT_MAX, INT_MAX, INT_MAX, INT_MAX, INT_MAX, INT_MAX, INT_MAX,INT_MAX},
                                {INT_MAX, INT_MAX, INT_MAX, INT_MAX, INT_MAX, INT_MAX, INT_MAX,INT_MAX},
                                {INT_MAX, INT_MAX, INT_MAX, 9, INT_MAX, INT_MAX, INT_MAX,5},
                                {INT_MAX, INT_MAX, INT_MAX, INT_MAX, 7, INT_MAX, INT_MAX,INT_MAX},
                                {INT_MAX, INT_MAX, INT_MAX, INT_MAX, INT_MAX, 8, INT_MAX,INT_MAX},
                                };
    int n = matrix.size();
    vector<vector<int>> minTree(n, vector<int>(n, 0)); //记录最小生成树
    Dijkstra(matrix, 0);


    return 0;
}

• 运行结果：

[z@r test]$ ./test 
0到1的最短路径为：0->1->权值和为：3
0到2的最短路径为：0->1->2->权值和为：7
0到3的最短路径为：0->3->权值和为：2
0到4的最短路径为：0->4->权值和为：3
0到5的最短路径为：0->1->5->权值和为：11
0到6的最短路径为：0->1->6->权值和为：4
0到7的最短路径为：0->1->5->7->权值和为：16

• 使用优先级队列实现的结果保持一致：好处是只需要遍历更新了权值的结果，不需要从0到n重新遍历。

void Dijkstra(const vector<vector<int>>& matrix, size_t startPoint) {
    int n = matrix.size();
    vector<int> dict(n, INT_MAX); // 记录每个顶点权值和的当前最小值
    vector<int> father(n, -1);
    vector<int> visited(n);
    vector<Edge> edge;
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            if(matrix[i][j] != INT_MAX) {
                edge.push_back({i, j, matrix[i][j]});
            }
        }
    }

    priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> minHeap;
    //默认排序规则，first由小（top）到大，若first相等按second排序
    //first最小路径值，sencond节点
    dict[startPoint] = 0;
    minHeap.push({0, startPoint});
    while(!minHeap.empty()) {
        int value = minHeap.top().first;
        int p = minHeap.top().second;
        minHeap.pop();
        
        if(visited[p]) continue; //访问过的点跳过
        visited[p] = 1;
        // if(value > dict[p]) { //结果可以等价以上两条
        //         continue; //若值大于则不记录
        //  }
        
        for(auto eg : edge) {
            if(eg.srcpoint == p ){ //找到与p相等的源点，计算到其对应点的权值和，
                int des = eg.despoint;
                int w = eg.weight;
                if(dict[des]  > dict[p] + w) {
                    dict[des] = dict[p] + w;
                    father[des] = p;
                    minHeap.push({dict[des], des});
                }
            }
            
        }
    }

    PrintShortPath(startPoint, dict, father, n);
}

:::

• Bellman-Ford算法：单源路径，权值可以为负数